Extending the Knuth Operator

I just learned about the Knuth up-arrow notation yesterday. Basically, Knuth's up-arrow is the answer to the question "What comes next in the sequence \((+, \times, \wedge)\)?" You could call it iterated exponentiation. Later operators in the sequence are called "higher-order", and may be defined in terms of the previous order function.

A while back a friend and I successfully extended derivatives and integrals to fractional orders for Fourier decomposable functions. (I wrote up the story in the first two pages of this document (PDF).) Brandon (the friend) went on to extend derivatives to complex orders. So, when I saw the Knuth operator, the first thing that came to mind was, what about fractional orders? This is like asking "what comes between \(+\) and \(\times\)?"

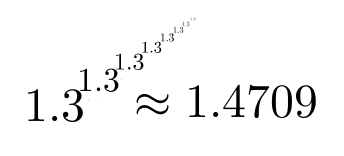
1.3 three-knuthed to the infinite power. It's finite! But, note that this is the infinite power that we are dealing with here, not infinite order. (The latter would be something else entirely, and I'm not sure that it would ever be nontrivially finite.)

I more clearly laid out what the Knuth operator is in an attachment Knuth Operator (PDF). What it would mean to extend the operator to non-natural orders is itself a nontrivial question, but that's part of the fun in finding the answer!

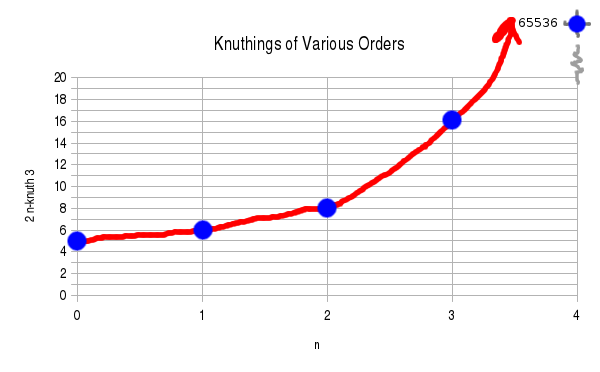
A plot of \(2\) n-knuth \(3\) for \(n = 0, 1, 2, 3, 4\). That is, we are plotting the n-th order Knuth operator to the base 2 and power 3. These values are drawn as blue dots. I would like to find some elegant extension to fractional orders. The curve will look something like the red hand-drawn curve in the figure.

---

Originally published on Quasiphysics.