Skip to content

research

NEMI 2025 Notes

tl;dr: I shared some work on counterfactual analysis of CoTs at a Mech Interp workshop, supported by a Cosmos+FIRE grant. See the technical details.

This year I had the pleasure of engaging in some mechanistic interpretability research. I was specifically curious about the causal structure of chain-of-thought reasoning used by models like OpenAI's o1 or DeepSeek's R1 to solve mathematical problems. What I learned is that these models' chains of thought are deceptively interpretable; that is, at first glance they appear to be thinking in human terms, but counterfactual analysis reveals the real mechanisms of "thought" to be far stranger, with a strong dependence on punctuation and certain expressions that mean to the model something other than what they would mean to a human.

The traditional autoregressive transformer architecture for a language model generates a single token in each forward pass. There is a certain amount of computation that can already happen in that single forward pass: models can add even several digit numbers together without any reasoning tokens or tool calls. However, more complex mathematical problems apparently exceed the computational power available in that single forward pass of the model. Reasoning models extend the compute available by generating a block of thinking tokens before giving the final answer. Through a training regimen pioneered by OpenAI in o1 and published openly by the DeepSeek team with their R1 paper, these models can be trained to do something that looks like reasoning, and it does well on mathematical benchmarks when the problems are similar to problems it has seen in training. As the training data is expanded, presumably with mid-training curricula interleaving mathematical and coding problems, these models are gaining significant utility in automating certain tasks in software engineering and assisted proof solving.

There are however serious shortcomings, one of which is that the models still make mistakes even on problems that we would expect to be well within the capabilities. We see this most starkly when working with a base model that has not been explicitly trained for reasoning, as you can read in my post on errors in DeepSeek V3 Base. (Incidentally, DeepSeek V3 Base may be the last model on which we can run this experiment: models trained after mid-2025 will likely contain examples of reasoning traces in their training data.) Reasoning models seem to make much of the same errors just at a somewhat lower rate, and buried deeper in their longer reasoning traces.

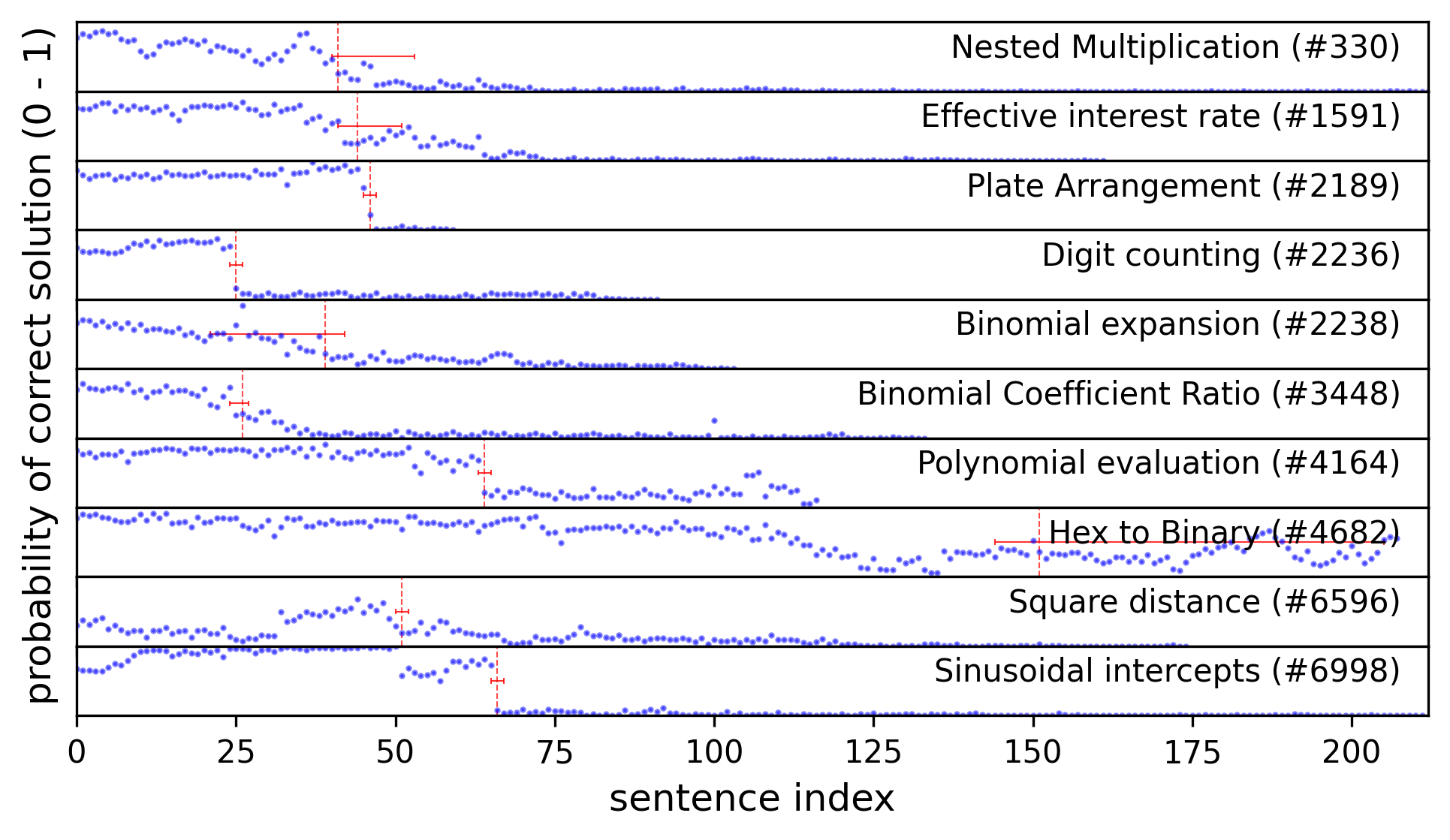
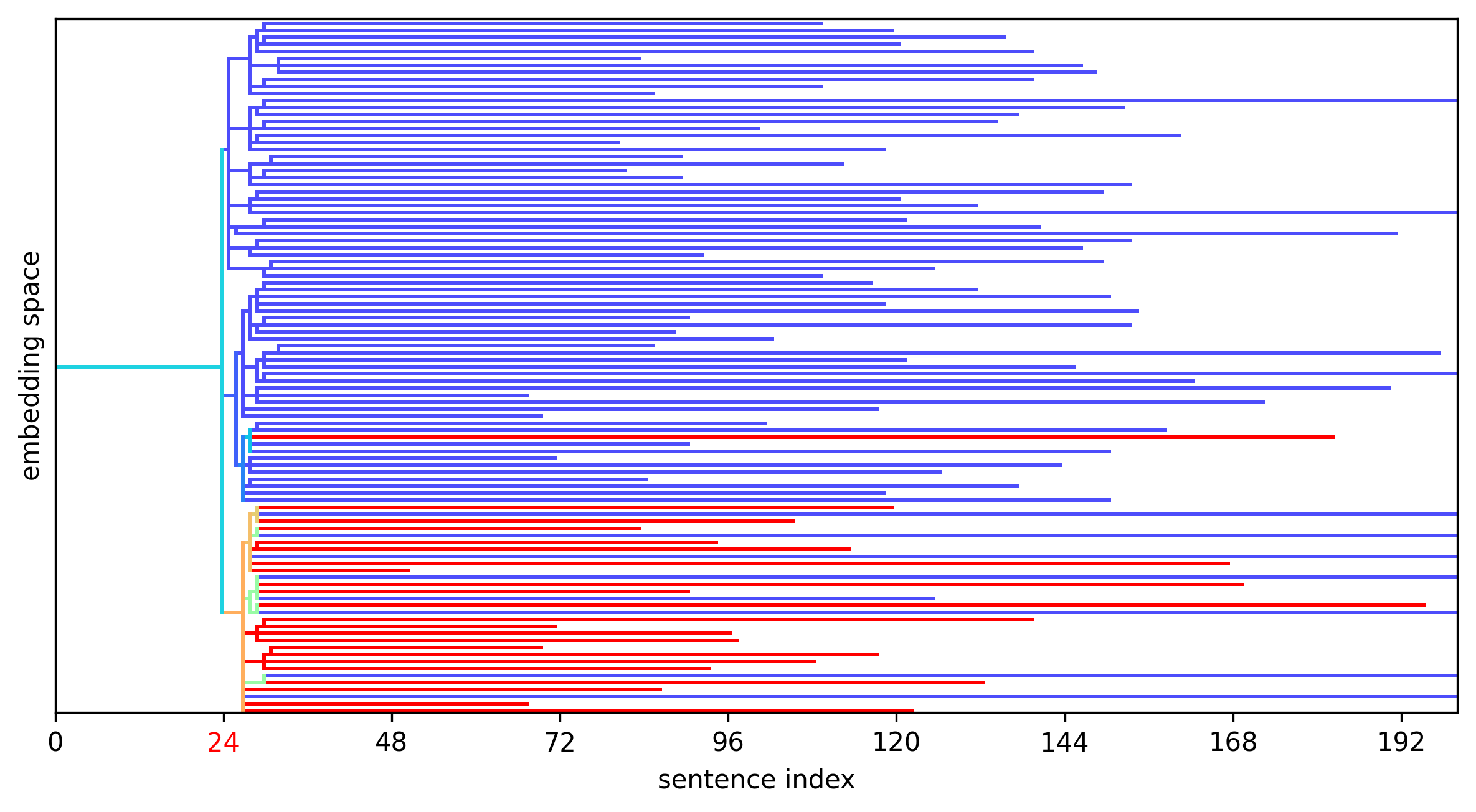
As I was working through some V3 Base traces manually, it occurred to me that it should be possible to find the exact location of the first error in a faulty chain of thought using counterfactual methods similar to what I had worked on some years earlier. I applied Bayesian changepoint detection and active sampling to quickly find the errors in traces of the recent Bogdan & Macar paper, and presented a poster on the topic at NEMI 2025.

At the NEMI poster session I met Eric Bigelow, whose work at Harvard took him down very similar paths, or I should say nearby Forking Paths. One of Eric's team's findings was that a lot of counterfactual weight was on punctuation marks. These "forking tokens" such as an opening parenthesis ( were likely to be places where the probability of successful answer changed precipitously. My work went down only to the sentence level rather than token level, so I cannot directly compare, but other work such as this paper by Chauhan et al. provides some more mechanistic explanation for how these punctuation marks function inside relatively small open-weight models.

I also had the opportunity to have an extended discussion with some folks on the research team at Goodfire who are doing interpretability as a service. Their focus seemed to be mostly on visual and bioinformatics models rather than reasoning, likely because the target market for MIaaS is more around domain-specific models that work in non-text modalities. Nonetheless I was able to rubber duck some things.

I was left with the impression that the line of inquiry I was following is impractical. The causal structure of chains of thought is just as messy as the weights inside the models. Although it appears easy to read, the actual workings are highly complex, inefficient, and alien. These so-called "reasoning" models are the latest search technology, and have their utility, but should always be paired with formal verification, and in cases where this is not possible, there is a great risk of biasing human readers with convincing-sounding model outputs.

I do believe that mech interp techniques can and should be applied to studying structure in CoTs, but this is not going to be easy, it just looks that way because the "thoughts" appear to be in English. (I am morbidly curious what the CoT would look like after applying strong optimization pressure to shorten the CoT while maintaining performance. Would RL/GRPO be sufficient to develop a shorthand language?)

Locating Reasoning Errors with Active Sampling

Chris Merck (chrismerck@gmail.com) -- 2nd North East Mechanistic Interpretability Workshop, August 22, 2025, Northeastern University, Boston

Abstract

Recent advances in chain-of-thought reasoning allow large language models (LLMs) to solve mathematical problems that are beyond the computational power of a single forward pass. This suggests the existence of learned mechanisms operating at the level of reasoning steps in the chain of thought (CoT), yet few techniques exist for identifying these mechanisms. Furthermore, chains of thought can be deceptively interpretable, resembling human internal monologues closely enough that we risk being misled about their causal structure, heightening the need for rigorous interpretability methods. In this work in progress, we develop an algorithm for locating reasoning errors in incorrect base solutions via targeted resampling. This exploration should improve our understanding of chain-of-thought reasoning, particularly how it goes wrong, allowing us to more safely and efficiently operate reasoning models.

Introduction

One frame through which to interpret reasoning traces is to treat them as the work of a math student, with the researcher as tutor. Correct answers to unguessable problems may be rewarded without inspecting the work, while the incorrect solutions are more interesting: the tutor scans for the first mistake and circles in red pen, leaving a helpful comment. We aim ultimately to automate this process, with this poster presenting some of the elements of work in progress. We see this work as part of a broad effort to take advantage of the present opportunity for CoT monitoring and interpretability (Korbak et al., 2025) and an application of counterfactual techniques from physical systems (Merck & Kleinberg, 2016).

Foundational Work. In their recent groundbreaking preprint, Bogdan et al. (2025) employ several techniques for finding causal structure among the sentences of a CoT reasoning trace, cross-validating counterfactual sampling against attention tracing and masking. They develop the math-rollouts dataset, containing 10 incorrect base solutions to problems from the MATH dataset as generated by DeepSeek R1-Distill Qwen-14B (DeepSeek, 2025), selected for intermediate difficulty (having between a 25% and 75% probability of being solved correctly). The dataset also contains 100 rollouts for each sentence in each reasoning trace, allowing us to explore the probability trajectory and counterfactual scenarios.

Active Bayesian Changepoint Detection

Although math-rollouts provides a useful starting point, we would like to eventually scale up to using state-of-the-art reasoning models where exhaustively generating many rollouts for each sentence would be prohibitively expensive. So we apply an active sampling algorithm to efficiently find the sentence containing the most prominent error, termed a changepoint after Adams & MacKay (2007), resulting in a ~100X reduction in the number of rollouts required, at least when the trace contains a clear error.

We propose a Bernoulli process model with a single changepoint τ at which the probability of a correct solution drops from p₁ to p₂:

\[ p(\text{correct}_t) = \begin{cases} p_1 & \text{if } t < \tau \\ p_2 & \text{if } t \geq \tau \end{cases} \]

Bayesian Inference. We maintain a posterior distribution over changepoint locations τ ∈ {1, …, T} using a uniform prior. For each hypothesis τ, we model the probabilities with Beta priors: p₁ ~ Beta(2, 2), reflecting our belief that the initial probability lies between approximately 25% and 75%, and p₂ ~ Beta(1, 19), a strong prior on a low chance of recovery.

Active Sampling. We select the next sample location with replacement to maximize expected information gain about the changepoint location:

\[ t^* = \arg\max_{t} \mathbb{E}_{y_t}[H(\tau) - H(\tau | y_t)] \]

where H(τ) is the entropy of the current posterior over changepoint locations and y_t ∈ {0, 1} is the correctness of the hypothetical resampled rollout. This strategy efficiently focuses sampling around the uncertain changepoint region.

Probability Trajectories. With the choice of a strong prior on p₂, we find that the algorithm tends to find reasonable changepoints with just 100 rollouts.

Probability trajectories for all 10 incorrect base solutions. Each subplot shows how chances of success evolve along the CoT. Red vertical lines indicate detected changepoints (80% CI).

Failure Analysis

We now examine and discuss selected failures based on the change in answer distribution at the changepoint and a reading of the trace.

Nested Multiplication (#330) — wrong base case in recurrence relation

Wait, wait, no. Let me think. Wait, in the original expression, each time it's 3(1 + ...). So, actually, each level is 3(1 + previous level). So, maybe I should approach it as a recursive computation.

The trace was on the right track—only two computations away from the correct answer. But when the model used the ellipsis (...), many rollouts failed to converge to a boxed answer, recursing until the token limit. The base solution does converge, and fails due to an error in the base case of 4 instead of 0 or 12. Although visually the probability trajectory does seem to contain a clear changepoint, the identified sentence is in fact by inspection the first introduction of this mistake that persists into the incorrect solution.

Now we examine the starkest failure in the Digit Counting problem:

Digit Counting (#2236) — non sequitur

The ones digits here are 1–8, so 4 doesn't appear in the units place in this partial set.

Here the model makes a statement that is obviously false to us, but is generated with approximately a 25% probability at this step. To better understand the structure of this failure, we collect all 100 rollouts resampled at this changepoint sentence and visualize them in a dendrogram. Following Bogdan et al. (2025), we join rollouts if the sentence embeddings have cosine similarity greater than the median similarity between all sentence pairs (0.8).

A visualization of the 100 resamplings at sentence 24. Color indicates the probability of a correct solution (blue = 1.0, red = 0.0). We observe that the resampled rollouts fall into three clusters, the bottom of which is the path taken in the incorrect base solution. The clear separation of the incorrect cluster demonstrates that the similarity metric is a good definition for the notion of "sameness" of a sentence.

Finally, we examine a case where there is no clear changepoint. Inspecting the the model's solution summary, we find that the model was quite knowingly vacillating between two possible interpretations of the problem:

Hex to Binary (#4682) — trick question

While converting each hexadecimal digit to 4 bits results in a 20-bit binary number, the minimal number of bits required to represent the number 419,430₁₀ without leading zeros is 19.

However, since the problem asks for the number of bits when the hexadecimal number is written in binary, and considering that each hexadecimal digit is typically converted to 4 bits, the correct answer is 20 bits.

Limitations and Future Directions

  • Although we prefer to investigate reasoning errors in a counterfactual context, there is a body of existing work that studies errors in chain-of-thought prompting within and beyond mathematical reasoning (Lightman et al., 2023; Tyen et al., 2024), which also examines reasoning structure beyond the influence on accuracy (Xia et al., 2025).

  • As we saw with the trick question, the failure of these models to deliver mundane utility often stems from issues interpreting the user's prompt rather than logical errors within the chain of thought. The relationship of user intent and model interpretation can be fully formalized (Wu et al., 2022) for mathematical problems. The broader problem of prompt interpretation is of high importance to alignment, especially as models become capable of achieving more work with a single operator instruction.

  • The rollouts in math-rollouts are drawn from a relatively small 14B model distilled from a larger one (DeepSeek R1 671B). It is possible that reasoning failures in stronger models are qualitatively different, or that the structure of the reasoning behavior differs after distillation. The changepoint detector introduced here is intended to facilitate testing on larger models.

  • The changepoint model assumes a single error. However, realistic chains of thought may contain multiple errors and backtracking leading to a more complex probability trajectory. It is possible to develop a changepoint detector for these more complex structures, but validation requires much more than the 10 examples available in the math-rollouts dataset.

  • In particular, the case of no clear changepoint is important to avoid spurious error detections. The algorithm could be updated to track confidence in a null hypothesis.

  • State-of-the-art reasoning models and agents use parallel execution and subagents (subroutines with chains of thought that are not fully attended to by the top-level agent such as in Anthropic, 2025). Investigating failure modes of these new architechtures is a challenge due to their complexity, however it would appear that the Bogdan et al. (2025) methods could be adapted. Active sampling may be of even greater importance as the compute per rollout increases.

Acknowledgements

I am grateful for discussions of this work with Anuj Apte. This work is generously supported by a grant from the Cosmos Institute (https://cosmos-institute.org/) and the Foundation for Individual Rights and Expression (FIRE) (https://www.thefire.org/).

References

  • Adams, R. P., & MacKay, D. J. (2007). Bayesian online changepoint detection. arXiv preprint arXiv:0710.3742.
  • Anthropic (2025). Claude 3.5 Sonnet with Computer Use. Available at: https://www.anthropic.com/
  • Bogdan, P., et al. (2025). Thought Experiments: Counterfactual Reasoning in Chain-of-Thought. arXiv preprint.
  • DeepSeek (2025). DeepSeek R1: Reasoning at the Edge of AGI. arXiv preprint.
  • Korbak, T., et al. (2025). Chain-of-thought reasoning as a monitoring opportunity. arXiv preprint.
  • Lightman, H., et al. (2023). Let's verify step by step. arXiv preprint.
  • Merck, C., & Kleinberg, S. (2016). Causal explanation under indeterminacy: A sampling approach. In Proceedings of the AAAI Conference on Artificial Intelligence.
  • Tyen, G., et al. (2024). LLMs cannot correct reasoning errors yet. arXiv preprint.
  • Wu, Y., et al. (2022). Autoformalization with large language models. arXiv preprint.
  • Xia, M., Li, X., Liu, F., Wu, B., & Liu, P. (2025). Reasoning structure in chain-of-thought beyond accuracy. arXiv preprint.